COMPETING
COMPARATIVE PROBLEMS EASILY EASY
Comparison
is the concept of comparing two or more magnitudes to see which one is greater,
whichever is smaller, how much difference, how much is it and so on. For
example, comparing the number of chickens with the price, many workers with
time finished work and others. The stratified comparison is comparing more than
two magnitudes, either three or four or more. For junior level, the stratified
comparison is only up to level three. Ability of average junior high students
still not good in solving the problem of stratified comparison of sola. This is
evident from the results of the UN 2017 yesterday which averages put a matter
of stratified comparison into the category of difficult questions. In this case
required a new breakthrough by us as a teacher or mathematical mathematics UN.
With such an easy solution it is expected that the matter of stratified
comparisons is no longer a scourge for our students. This opportunity allows
admins to share the multilevel comparative learning experiences that our students
find far more easily understood
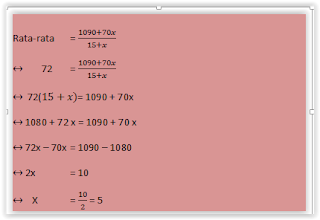
Problem-comparison comparison of multilevel has two categories, then admin will give an example. Of course, about the problem that we discussed become an important part in the Grid of the National Examination from 2016 until 2019 using SKL slices of curriculum 2006 and the curriculum 2013, about the matter of storied comparison will always come out adorn the queried about the National Exam junior high. Immediately, we go to the example of multi-level comparisons. A. Category matter first tiered comparison 1. Comparison of money A and B is 2: 5, while the ratio of money B and C is 3: 4. If the sum of money them three Rp820.000,00, then the difference of money A and C is .... A. Rp100.000 , 00 C. Rp280.000,00 B. Rp180.000,00 D. Rp300.000,00
Solved
Then A: B: C = 6: 15: 20
(6 + 15 + 20) / (20-6) = (820 000) / x
41/14 = (820 000) / x
X = (820 000 x 14) / 41 = 280 000, where x is the difference A with C
So the difference A with C is Rp 280.000,00
Categories of second-tier comparison
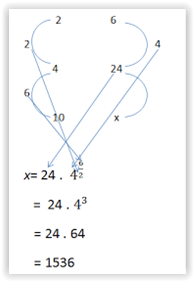
The comparison of Furqon, Aldi and Hidayat marbles is 4: 1: 5. If the difference between many
marbles Hidayat and aldi 320 grains, the number of marbles they ...
540 items640 items800 items900 itemsAnswerDifference between Hidayat and Aldi = 4Difference of marbles Hidayat with Aldi = 320Number of Third Comparisons = 10Number of marbles three = x4/320 = 10 / xx = (320 x 10) / 4 = 800 items
Let's practice the matter of otherstratified comparisons.
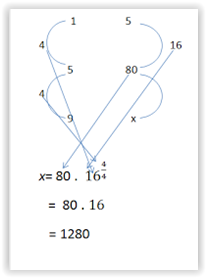
1. Comparison of money A: B: C is 6: 3: 5. If the amount of money A and C is Rp88.000,00,
then the amount of money is three ....
A. Rp122.000,00
B. Rp102.000 , 00
C. Rp112.000,00
D. Rp92.000,00
2. Comparison
of money Beni and Rita money is 2: 3, while the ratio of money Rita and Susi 4 : 5. If their money
amount Rp140.000,00, then the difference between Rita and Susi money is ....
A. Rp12.000,00 C. Rp28.000,00
B. Rp16.000,00 D. Rp32.000,00
It's easy to do. Hopefully with this simple way learners will be easy in
solving this stratified comparison problem easily